Los engranes
Los engranes se emplean comúnmente para transmitir fuerza de una flecha que gira a otra. En comparación con las transmisión por ficción o bandas, se diferencian en que se adaptan especialmente donde se requiere una relación exacta de velocidad, o donde la relación entre los miembros motriz y movido accionado deben de conservar una relación definida de fase. Como la acción enclavada de los dientes logra una transmisión positiva, y no se depende de la ficción para evitar el resbalamiento, la fuerza necesaria para mantener los engranes en posición cuando se esta transmitiéndola fuerza es mucho menor que en una trasmisión equivalente de fricción. Esta da por resultado menores presiones en los puntos de apoyo, menor desgaste en las
superficies de los cojinetes, y una mayor eficiencia.
Superficie primitiva: La superficie primitiva de los engranes se define como una superficie imaginaria que gira conjuntamente con otra sin resbalamientos, semejante a los cuerpos circulares con rodamiento friccional. Para cualquier tipo de engrane se debe conocer la forma y dimensión de la superficie primitiva antes de que se puedan diseñar los dientes apropiados. La Fig. 9.1 muestra la superficie primitiva circunferencial para un engrane.
Elementos del diente: El diente de un engrane se puede considerar compuesto de superficies cursadas por una línea que se mueve a través del espacio. No siempre la línea es una recta o ni siquiera de forma regular.
Estas superficies generatrices en cualquiera de sus posiciones consecutivas son conocidas como los elementos del diente. Los elementos del diente siempre conectan puntos correspondientes, sobre secciones del diente de un engrane, que son líneas rectas paralelas unas a las otras.
Las ruedas dentadas son ilustraciones de pares superiores, porque se obtiene únicamente
contacto en una línea o un punto.
Clasificación de los engranes
Los engranes pueden ser clasificados de diferentes formas. Una manera de clasificar los engranes es de acuerdo con la posición relativa de los ejes de revolución. Los ejes pueden ser
a) paralelos (engranes común, helicoidal y en ángulo)
b) que se intersectan (engranes cónico recto y en espiral)
c) que no se intersectan ni son paralelos o ejes que se cruzan (engranes helicoidal, tornillo sinfín e hipoides)
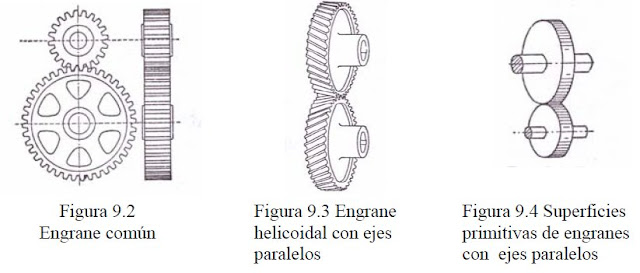
a) Engranes para conectar flechas paralelas: Aquí podremos emplear el engrane común como el
ilustrado en la Fig. 9.2 o los engranes helicoidales con ejes paralelos de la Fig. 9.3. En ambos, las superficies primitivas son circunferenciales con contacto con rodamiento pudo como lo ilustra la Fig. 9.4.
El engrane helicoidal trabaja con mucho menos ruido que el otro tipo y la diferencia a este respecto es particularmente notable a alta velocidad. La desventaja del engrane helicoidal consiste en el empuje final producido cuando el engrane esta transmitiendo la potencia. Con los engranes en ángulo (figura 9.5) el empuje final producido a un lado, es balanceado por otro empuje igual y opuesto ocasionado por la acción del otro lado. Estos engranes se pueden considerar como si fueran compuesto de los engranes helicoidales de dimensiones semejantes, uno teniendo una hélice derecha y el otro una izquierda.
b) Engranes para ejes que se intersectan: En este caso se emplean los engranes cónicos rectos, ilustrados en la fig. 9.6, o los engranes cónicos en espiral mostrados en la Fig. 9.7. En ambos casos las superficies primitas tienen un ápice común como lo indica la Fig. 9.8.
En el caso de los engranes cónicos rectos, los elementos del diente son líneas rectas, mientras que en los engranes cónicos en espiral los dientes son inclinados al eje y curvos. Los engranes cónicos en espiral tienen decididamente una ventaja sobre los engranes cónicos rectos por ser de operación silenciosa, similarmente a la ventaja que tienen los engranes helicoidales sobre los engranes comunes.
Un par de engranes cónicos que son del mismo tamaño y sus flechas ser intersectan a un ángulo recto se conoces como engranes a escuadra. Su uso principal es el retransmitir el movimiento alrededor de una esquina sin alterar la velocidad angular.
c) Engranes para conectar flechas que no se intersectan ni son paralelas: Aquí los engranes helicoidales con ejes que se cruzan, los tornillos sinfín o los engranes hipoides son los apropiados.
Los engranes helicoidales con ejes que se cruzan (Fig. 9.9) se emplean para conectar flechas que no son paralelas ni se intersectan. Sus superficies primitivas son cilindros (fig. 9.10). Se tocan en un punto y tienen contacto con deslizamiento ; por esto los dientes también hacen contacto en un punto y tiene una componente en deslizamiento a lo largo de la hélice del diente.
El tornillo sinfín, mostrado en la Fig. 9.11 es una forma especial del engrane helicoidal, los dos miembros se conocen como el sinfín y la rueda serpentina o corona. El sinfín, comparado con un engrane helicoidal tienen un gran distancia alrededor de la circunferencia. Es una costumbre denominar los dientes del tornillo sinfín “hilos” por su semejanza con un perno encordado. Por esto nos referimos a un “tornillo sinfín de un hilo” , “un sinfín de dos hilos”, etc., dependiendo del número de dientes formados en la superficie cilíndrica.
La rueda serpentina puede tener la superficie de los dientes cóncavos como lo muestra la Fig. 9.11 con el propósito de obtener un contacto lineal de los dientes en vez de que este sea un punto. La configuración de las superficies primitivas de un tornillo sinfín se muestran el a Fig. 9.12.
Los engranes hipoides ( figura 9.13) se parecen un poco a los engranes cónicos en espiral en su apariencia general. El contacto entre las dos superficies primitivas ocurre sobre una línea común a las dos rotaciones.
relación de velocidad
Una regla para un par de ruedas dentadas es que la relación de velocidad angular es inversamente proporcional al número de dientes. Esta regla es aplicable a todas las clases comunes de ruedas dentadas, tales como engranes comunes, cónicos y engranes helicoidales.
Cuando dos engranes se encuentran en movimiento, es evidente que el mismo número de dientes en cada engrane pasa por cualquier punto fijo durante un intervalo definido de tiempo, en vista de que los dientes de un engrane embonan en orden consecutivo con los huecos o espacios entre los dientes del otro engrane. Un engrane que tiene N2 dientes efectúa una revolución mientras N2 dientes que pasan por un punto fijo. Un engrane con N3 dientes engranado con el anterior harán consecuentemente N2/N3 revoluciones durante el mismo intervalo.
Si ω2 y ω3 son las velocidades angulares respectivas de dos engranes, entonces,
Lo que comprueba la regla anterior.
Terminología de los engranes
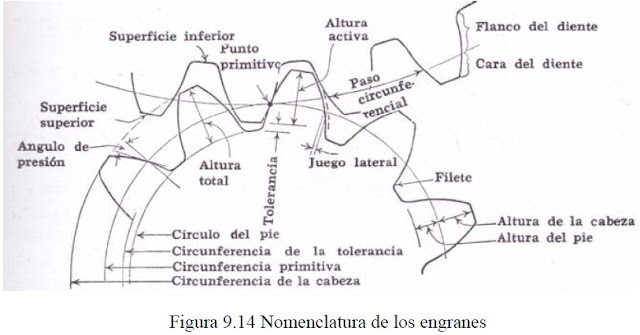
La Fig. 9.14 ilustra casi todas las siguientes definiciones:
Diámetro primitivo o diámetro de paso: El diámetro del cilindro que es la superficie primitiva de un engrane se conoce como diámetro primitivo o diámetro de paso. Ya que las superficies primitivas de dos engranes giran juntas sin resbalamiento, constituyen superficies con contacto de rodamiento puro y la relación de velocidad angular es en proporción inversa a los diámetros primitivos. Un par de engranes correlativos tiene el número de dientes proporcional a sus superficies primitivas, porque ambos deben tener el mismo paso de los dientes en orden de obtener rodamiento puro de las superficies primitivas. Entonces para estos engranes, 2 y 3,
donde N, D y ω representan, respectivamente, el número de dientes, el diámetro primitivo o de paso y la velocidad angular.
Punto de contacto primitivo: Aquel punto sobre la línea que une los centros de dos engranes en donde los círculos primitivos son tangentes se denomina punto de contacto primitivo.
Addendun o altura de la cabeza del diente: La distancia desde el circulo primitivo hasta el extremo exterior del diente, medido radialmente, se conoce como addendum o altura de la cabeza del diente.
Dedendum o altura del pie del diente: La altura del pie del diente es la distancia radial desde el circulo primitivo hasta la circunferencia del fondo del pie del diente.
La altura total: Es la suma de la altura de la cabeza del diente más la altura del pie del diente, o sea la suma del addendum y dedendum.
Juego de fondo: El juego de fondo es el espacio muerto que libran las puntas de los dientes de un engrane entre los hechos correspondientes de otro engrane, es decir la holgura entre la punta de un diente y la circunferencia de fondo. Y esta se mide sobre la línea de centros.
La altura activa: Es la altura total menos el juego de fondo.
Juego lateral: La distancia mínima entre el lado no motriz de un diente y el lado opuesto del diente en el engrane adjunto se denomina juego lateral o sea la diferencia entre el hueco y el espesor del diente. Esto se mide sobre el círculo primitivo.
La cara del diente: Es la superficie de un diente entre el círculo primitivo y el círculo formado a la altura de la cabeza del diente.
El espesor de la cara: es el ancho del engrane medido sobre la superficie primitiva en un plano conteniendo el eje de rotación. La cara de un diente no debe confundirse con el espesor de la cara, ya que son dos cosas enteramente dientes. La primera es una superficie y la última una dimensión.
El flanco del diente: Es la superficie de un diente entre el círculo primitivo y la circunferencia de fondo.
La superficie superior: es la superficie plana de un diente entre las caras del mismo diente.
La superficie inferior: es la superficie de un engrane entre los flancos de dientes adjuntos de un mismo engrane.
El filete: es la superficie curva que une el flanco de un diente con la superficie inferior. Coincide entre el juego de fondo y la circunferencia de fondo.
El Angulo de presión de un diente: es el ángulo que se forman entre el perfil del diente y una línea radial que se intersecta con la circunferencia primitiva.
Engrane y Piñón: Cuando dos ruedas dentadas se encuentran engranadas una a la otra, comúnmente se refiere uno a la mayor como “el engrane” y la menor como “el piñón”.
Cremallera: Cuando se cortan dientes sobre una barra recta, esto se conoce como cremallera. La Fig. 9.15 muestra un piñón y una cremallera. La superficie primitiva de la última es un plano.
Angulo y arco de acción: El ángulo que gira la rueda motriz durante el periodo en que uno de sus dientes permanece en contacto con el otro diente de la rueda accionada se conoce como el ángulo de acción de la motriz. El ángulo girado por la rueda accionada durante el mismo periodo de tiempo es el ángulo de acción de la rueda movida. Los arcos correspondientes sobre la circunferencia primitiva se denominan arcos de acción.
Evidentemente el arco de acción debe ser mayor que el paso circunferencial; de otra manera el contacto entre un par de dientes cesaría antes de que el siguiente par entre en contacto. En general, mientras mas grandes son los dientes, mas grande debe ser el arco de acción. Esta consideración ha sido el factor importante para fijar el tamaño de los dientes a un tamaño normalizado.
La relación de contacto: es un a medida del promedio del número de dientes en contacto en un par de ruedas dentadas engranadas y es igual al arco de acción dividido entre el paso circunferencial. El ángulo de acceso, es el ángulo girado por un engrane, desde el instante que un par de dientes entran en contacto, hasta el instante en que estos mismos dientes están en contacto sobre el punto primitivo.
El ángulo de receso: es el ángulo girado por un engrane desde el instante en que un par de dientes hacen contacto en el punto primitivo hasta el instante que cesa el contacto entre los dientes.
El ángulo de acción: es la suma de los ángulos de acceso y receso.
Paso
El paso de un engrane es una medida del tamaño de los dientes; todas las dimensiones de los dientes en sistemas normalizados están basadas en el paso . Los engranes que se pretenden hacer girar uno sobre otro deben tener el mismo paso, así como también los perfiles de los dientes de la debida forma. A continuación damos los métodos comunes para indicar el paso de los engranes:
El paso circunferencial: es la distancia que separa puntos correspondientes de dientes inmediatos, esta distancia se mide sobre la circunferencia primitiva. Entonces si p indica el paso circunferencial, D el diámetro primitivo o de paso y N el Número de dientes:
El paso diametral: (Módulo) es el resultado que se obtiene al dividir el numero de dientes entre el
paso circunferencial.
Definido de otra manera sería, el número de dientes por pulgada del diámetro de su
circunferencia primitiva.
El paso diametral Pd se expresa por la ecuación.
Debe observarse que el paso circunferencial es una dimensión lineal, expresada comúnmente en pulgadas. Las unidades del paso diametral son recíprocas de las pulgadas. De cualquier forma, es una costumbre indicarlas como un número o una relación. La Fig. 9.16 nos es útil para visualizar el tamaño de los dientes con varios pasos diametrales.
Puede observarse que la relación entre el paso circunferencial y el paso diametral se obtiene al multiplicar las dos ecuaciones, obteniéndose: p Pd = π
El método del paso circunferencial para especificar el tamaño de los dientes es el mas antiguo, pero el método del paso diametral tienen ventajas que han resultado muy prácticas para el uso general y especialmente donde se requieren dientes muy pequeños. A continuación se muestra una ventaja: un engrane con 19 dientes de 2 pd tienen un diámetro primitivo de 19/2=9 ½ plg. (24.13 cm) según la ecuación del paso diametral. Un engrane con 19 dientes y de 2 plg de paso circunferencial tiene un diámetro primitivo de (19 X 2)/ π = 12.095+ pulg. (30.7213 cm) según Figura 9.16 Tamaño de los dientes con pasos diametrales normalizados la ecuación de paso circunferencial. Es mucho mas fácil el cálculo con el método anterior y el
resultado siempre es un número racional. Por lo general, el paso circunferencial se emplea para especificar dientes de engranes de grandes vaciados y de algunos sinfines, mientras que el paso diametral se usa para todos los otros engranajes.
En Europa, el método de clasificar consiste en especificar la relación del diámetro de paso con
respecto al número de dientes, y a esta relación se le denomina módulo. Por lo tanto, el módulo es
el recíproco del paso diametral y se expresa como:
Los valores numéricos de los módulos se especifican en unidades de milímetros.
Debe notarse que el paso diametral y el módulo de definen como relaciones y no son distancias físicas que se puedan medir en un engrane. El paso circunferencial, por el contrario, se definió como la distancia medida a lo largo del circulo primitivo desde un punto en un diente hasta el punto correspondiente en el siguiente diente.
Para fines de especificar los cortadores de engranes, los valores del paso diametral y del módulo se tomaron generalmente como números enteros.
Ley fundamental del engranaje
Los engranes son generalmente secciones circulares y dan una relación constante de la velocidad angular de las flechas que conectan, aunque hay engranes que no son circulares, que se emplean cuando se necesita una relación de velocidad variable. Sean circulares o no, los dientes deben de ser de tal forma que e produzca un contacto con rodamiento pudo de las superficies primitivas.
Por lo anterior, las superficies primitivas se someten a las leyes que gobiernan los cuerpos que tienen contacto con rodamiento puro de las superficies primitivas. Por lo anterior, las superficies primitivas se someten a las leyes que gobiernan los cuerpos que tienen contacto con rodamiento puro, discutidas en el Cáp. 8. Por lo anterior el punto de contacto de dos perfiles primitivos, conocido como punto de contacto primitivo, es un centro instantáneo común a los dos engranes.
Si los dientes de un engrane se diseñan de tal forma que se obtienen un rodamiento puro de las superficies primitivas, entonces resulta las siguiente ley para los dientes de los engranes:
“La normal común a las superficies de los dientes en el punto de contacto siempre debe pasar a través del punto de contacto primitivo”.
Esta ley se comprueba como sigue: la Fig. 9.17 muestra dos dientes haciendo contacto en C. Considerando estos engranes 2 y 3 y la bancada 1 en la cual giran como tres cuerpos que tienen movimiento relativo, es posible localizar sus centros instantáneos. Por lo tanto es obvio que O21 y O31 se localicen en los centros de giro de 2 y 3 respectivamente.
Los dientes correspondientes son dos cuerpos en contacto con deslizamiento en C; por esto el movimiento relativo en el punto de contacto es sobre la tangente común LM; de otra forma el diente tendría la tendencia a interferir o roer el contacto. Por lo anterior, el centro instantáneo O23 debe de coincidir sobre la normal común XY. Por el teorema de Kennedy también debe de coincidir sobre la línea que pasa a través de O21 y O31. por tanto el centro instantáneo O23 coincide con punto P.
Para cuerpos con rodamiento:
Si esta relación se mantiene constante, entonces el centro O23, o sea el punto P, debe de mantener una posición fija; y P es el punto de contacto de las dos superficies primitivas o el punto de contacto primitivo.
Acción con deslizamiento de los dientes
Cuando un par de dientes hacen contacto en el punto de contacto primitivo, tienen por un instante, contacto con rodamiento puro, ya que el punto de contacto es en ese momento un centro instantáneo para los engranes. Por lo que se sigue que en cualquiera otra posición deben de deslizarse uno sobre el otro, porque entonces se encuentran en otro punto que no es el centro instantáneo. La velocidad del deslizamiento esta en proporción directa a la distancia desde el centro instantáneo hasta el punto de contacto en el instante considerado. La velocidad máxima del deslizamiento ocurre cuando justamente empieza o termina el contacto entre los dientes , estando entonces el punto de contacto lo mas alejado del punto de contacto primitivo.
La magnitud de la velocidad de deslizamiento se puede determinar en cualquier instante gráficamente.
En la Fig. 9.18 se ilustra un par de dientes conjugados haciendo contacto en el punto C.

La normal común sobre C es la línea XY, que pasa a través del punto de contacto primitivo. La velocidad lineal de C, considerado como un punto sobre el engrane 2, se representa por el vector CE perpendicular al radio CA. La velocidad de C, considerando como un punto sobre el engrane 3, se representa por el vector CD, perpendicular a CB. Los vectores CE y CD pueden resolverse en componentes paralelas a XY de cada unos, deben tener la misma velocidad normal Vn, ya que los dientes permanecen en contacto y aun no encajan uno dentro del otro. La diferencia algebraica de los componentes de velocidad perpendiculares XY, es decir, DE = FD-FE, representa la relación de deslizamiento de una superficie sobre la otra o la velocidad de deslizamiento. Una inspección a la figura mostrará que esta velocidad disminuye cuando el punto de contacto se mueve hacia el punto P y aumenta cuando se mueve en la dirección opuesta.
Perfil del diente
Por lo general, es posible seleccionar los dientes de cualquier forma un engrane y después proceder a construir los dientes para un segundo engrane, el cual será conjugado con el primero, cumpliendo con las leyes fundamentales del engranaje. Si se selecciona la forma al azar, y se construye un diente conjugado de la forma o perfil teóricamente correcto, no resultaría necesariamente práctico el uso de tales dientes.
Haciendo a un lado el hecho, que la superficie de trabajo de los dientes de un engrane deben cumplir con la ley fundamental, muchos otros requisitos han afectado la selección del perfil de un diente para un engrane de proporciones normalizadas.
a) El diente debe de estar capacitado para ser producto con precisión y a bajo costo.
b) La forma o perfil debe tener buenas cualidades para resistir el desgaste. Las velocidades reducidas para el resbalamiento y un acceso próximo a la superficie de contacto son dos condiciones favorables. La última condición se obtienen cuando ambos dientes correspondientes tienen un gran radio de curvatura. Las presiones sobre el diente se distribuyen sobre un tramo ancho de la superficie cuando se emplea un gran radio de curvatura. El resultado es una menor intensidad de presiones y menos desgaste.
c) Con el perfil del diente debe de conseguirse una buena “resistencia medular”. Durante el servicio hay fuerzas que actúan sobre el flaco del diente que tienden a doblarlo como un trabe. La resistencia medular es mayor en un diente pequeño con una sección ancha a lo largo del fondo.
d) El arco de contacto debe de ser cuando menos igual al circulo primitivo; de otra manera no habría un contacto continuo entre los engranes. Un arco de acción mayor de 1.4 veces el círculo primitivo generalmente se considera como un buen diseño. Debajo de este límite, resulta una acción muy ruidosa, a menos que los dientes sean cortados con mucha rescisión.
e) Generalmente es aconsejable el intercambio de una seria de engranes del mismo paso, no obstante esto no es necesario con muchos engranes que son del tipo “propósito especifico”. La aplicación cicloide se utilizó ampliamente para perfiles de dientes, pero ha sido enormemente reemplazada por la envolvente.
De las muchas formas posibles que puede tener un diente únicamente se han estandarizado la forma cicloide y la involuta o evolvente. La cicloide se empleo inicialmente, ahora se ha reemplazado con la involuta en la mayoría de las aplicaciones excepto en los relojes de pulso y pared. La involuta tiene varias ventajas, siendo las más importantes su facilidad de fabricación y el hecho de que la distancia entre los centros de dos engranes de involuta puede variar sin cambiar la relación de velocidades. A continuación se describirán los detalles más importantes de estos dos engranes.
Dientes cicloidales
La cicloidal es una curva descrita por un punto sobre un círculo que rueda interiormente o exteriormente sobre otro círculo.
El círculo que rueda es conocido como el círculo descriptivo, o ruleta y en la formación del perfil del diento de un engrane, rueda interiormente y exteriormente sobre el círculo primitivo. El rodamiento interno forma el flanco del diente; el externo forma la cara.

En la Fig. 9.19, a y b, son círculo primitivos de los engranes; c y d son los círculos descriptivos o ruleta. El circulo c rueda interioramente sobre a, el punto P sobre c describe la curva PB, la cual forma el flanco del diente en la rueda superior. Entonces el círculo c rueda exteriormente sobre b y el punto P sobre c traza la curva PC, la cual es la cara del diente sobre el engrane inferior. De la misma manera, las curvas PD y PE se obtienen haciendo girar el círculo d interiormente sobre b y exteriormente sobre a. Estas curvas forman, respectivamente, el flanco del engrane inferior y la cara del superior. No necesitan ser los dos círculo descriptivos iguales, pero debe emplearse el mismo círculo para obtener la cara de un diente y el flanco del otro que trabaja o corresponde con él. En la práctica, para obtener intercambio de los engranes, se emplea a través de una serie el mismo radio de los círculos descriptivos o ruletas.
Cuando el diámetro de la ruleta o círculo descriptivo es la mitad del diámetro de la superficie primitiva del engrane, el flanco del diente se convierte en una línea recta radial (véase PB, Fig. 9.19) y el diente es un poco más angosto en la circunferencia de fondo. Si la ruleta o círculo descriptivo se hace más grande el diente continúa estrechándose en la circunferencia de fondo y le resta fuerza; también si el círculo descriptivo se fabrica lo suficientemente amplio, se hace imposible cortar los dientes del engrane por medio de una fresadora, porque el espacio entre los dientes se ensancha desde el círculo primitivo hasta la circunferencia de fondo.
Trayectoria de contacto
En la Fig. 9.20 un par de perfiles correspondientes de dientes del tipo cicloidal se ilustra en tres posiciones: o sea a1b1 cuando justamente están haciendo contacto; a2b2, cuando hacen contacto en el punto de contacto primitivo; y a3b3 cuando esta justo para romper el contacto.
La trayectoria del punto de contacto debe ser la cuerva CPD, la cual esta compuesta de las secciones de la circunferencia de los dos círculos generativos con centros en L y M.
El punto C done empieza el contacto se encuentra localizado en la intersección del círculo descriptivo superior con el circulo addendum o de la altura de la cabeza del diente del engranaje.
Mientras que D se encuentra en la intersección del círculo descriptivo interior con el circulo addendum del piñón. Alargando los dientes mueve evidentemente los puntos CD apartándolos mas y aumentado el periodo de contacto. Uniendo CP y dibujando PE perpendicular a la línea de centros AB, localizándole ángulo de presión CPE para la posición de los engranajes en la cual C es el punto de contacto. Este ángulo se disminuye cero cuando el punto de contacto se aproxima a P y de allí en adelante se aumenta a otro máximo hasta D.
Por lo anterior la forma cicloidal del diente se caracteriza por un ángulo de presión variable, el cual es cero cuando los dientes hacen contacto en el punto diametral.
Ángulos de acceso y receso
Refiriéndonos una vez mas a la Fig. 9.19 ya que a1a2, y a3 representan tres posiciones para el mismo diente sobre el piñón, O1; P, O3 son tres posiciones de un punto sobre el diente y los ángulos O1AP y PAO3 muestran los movimientos angulares correspondientes del piñón. Estos ángulos son respectivamente, los ángulos de acceso y de receso del piñón.
Desde los puntos Q1PQ3, los ángulos Q1BP de acceso de acceso y PBQ3 de receso del engranaje son localizados.
Los arcos de acción son los mismos para ambos, el engrane y el piñón, son iguales para O1O3. para Q1Q3.
Ventajas de los engranes cicloidales
Aunque los engranes cicloidales han sido reemplazados en gran medida por los de involuta, el perfil cicloidal tiene ciertas ventajas que vale la pena señalar. Estas se mencionan brevemente a
continuación.
Los engranes cicloidales no presentan interferencias, además de que un diente cicloidal generalmente es más fuerte que uno de involuta debido a que tiene flancos extendidos en comparación con los flancos radiales de un diente de involuta. Adicionalmente los dientes cicloidales tienen menos deslizamiento, y en consecuencia, menos desgaste. Sin embargo, una desventaja importante de los engranes cicloidales es el hecho de que para un par de engranes cicloidales solamente hay una distancia entre centros teóricamente correcta para la que trasmiten movimiento a una relación de velocidad angular constante. Otra desventaja es que aunque es posible fresar un engrane cicloidal, la fresa no se fabrica tan fácilmente como en el caso de una
fresa de involuta debido a que los dientes cicloidales de cremallera no tienen lados rectos como los dientes de involuta de cremallera. Debido a esta razón es posible construir dientes los engranes de involuta con mayor exactitud y economía que los cicloidales.
Los engranes de involuta han reemplazado completamente a los engranes cicloidales para la transmisión de potencia. No obstante, los engranes cicloidales se usan ampliamente en los relojes de pulso y de pared y en determinados instrumentos en los casos en que los problemas de interferencias y resistencia es de interés primordial. En los relojes, el tren de engranes desde la fuente de poder al escape, aumenta su relación de velocidades angulares con el engrane moviendo al piñón. En un reloj de pulso, este aumento puede llegar a ser hasta de 5000:1. En consecuencia los engranes serán tan pequeños que para evitar usar dientes excesivamente pequeños es necesario usar piñones (que son los engranes movidos en esta caso) que tengan apenas seis o siete dientes. Además el perfil del diente de estos piñones deben poder actuar en 60º de rotación. Debido a lo anterior se prefieren los dientes cicloidales sobre los engranes de involuta. El problema de la distancia entre centros y de la relación de velocidades angulares no es importante en este caso debido a que todo el tren, que es gobernado por un escape, queda en reposo y vuelve a entrar en movimiento varias veces por segundo. En consecuencia, la operación del tren involucra cambios tan grandes de momentum que el efecto de la forma del diente en este cambio es despreciable.
Dientes evolventes o de involuta
En general, si tomamos una línea recta y la arrollamos sobre una curva de cualquier forma, un punto sobre esta línea trazará una trayectoria conocida como la evolvente de la cuerva. Para casi todos los engranajes con dientes evolventes, la evolvente se forma arrollando una línea recta sobre un circulo. Las únicas excepciones son los engranajes que no tienen forma circular. Cuando hablamos de una evolvente refiriéndonos a los engranajes, sin mas definición, queremos decir la evolvente de un círculo. A este se le denomina comúnmente el círculo base de la evolvente o involuta.
Desarrollo mecánico de las curvas evolventes o involutas
Un dispositivo, ilustrado en la Fig. 9.21 ilustra un método para el desarrollo conjugado de las curvas evolventes. Una cuerda CD y C´D´ es arrollada alrededor de los dos discos circulares 2 y 3. El disco 2 tiene una placa transparente m adjunta a su cara, y 3 tienen una placa semejante n sujeta a él. Si 2 gira, la cuerda que actúa como una banda moverá a 3 en el sentido opuesto. Un punto R sobre la cuerda trazará entonces sobre la placa m una evolvente KL, y sobre la placa n una evolvente MN. Conservando 2 y 3 en una posición fija y entonces cortando la cuerda en R, las mismas curvas podrán ser trazadas por las dos puntas cuando las partes sueltas son enrolladas sobre y desenrolladas de los discos a los cuales se encuentran adjuntos.
Considerando los métodos anteriores para obtener las curvas, se hacen evidentes dos factores:
a) que el punto de contacto siempre cae sobre la línea de la cuerda: es decir, sobre CD;
b) que, en vista de que la sección de la tangente de la cuerda siempre esta columpiándose con referencia a un disco sobre un punto de tangencia con el disco en cuestión, el movimiento relativo siempre es perpendicular a la línea de tangencia.
Por lo anterior CD es la normal común a las dos curvas todo el tiempo y cruza la línea de centros en el punto fijo P. Además, la línea de acción hace un ángulo constante DPQ con la normal PQ a la línea de centros de los discos y para el diámetro determinado del disco y la distancia centro, el ángulo DPQ es el ángulo de presión.
En resumen, se ha comprobado que los perfiles evolventes:
a)conservan los requerimientos de la ley fundamental del engranaje.
b) tienen una trayectoria de contacto en línea recta.
c)tienen un ángulo de presión constante para una instalación determinada.
El punto P (Fig. 9.21), donde la línea CD intersecta la línea de centros, es el centro instantáneo de las ruedas 2 y 3 por lo tanto la relación de velocidad angular ω2/ω3 es igual a PB/AP, y por consiguiente P es el punto de contacto primitivo.
Cuando el punto de contacto primitivo P y el ángulo de presión son conocidos, se pueden localizar los círculos bases ya que son tangentes a la línea CD, cuya posición es fija para estos datos.
La acción del diente: En la Fig. 9.22 se ilustra un par de perfiles evolventes para un engranaje en tres posiciones. Consideraremos que los engranes giran como queda indicado por las flechas en el diagrama. En a1b1 los dientes empiezan justamente a hacer contacto; en a2b2 los dientes hacen contacto en el punto de contacto primitivo y en a3b3 el contacto esta a punto de terminar.
El punto de contacto siempre debe coincidir durante todo el tiempo sobre la línea recta CD, siendo esta línea la tangente común a los circulo base. El contacto empieza en F y termina en G. En el círculo primitivo P1, P2, P,3, del engrane superior representan las posiciones correspondientes de un punto en este engrane mientras que Q1P2Q3 son las tres posiciones semejantes ocupadas por un punto en el engrane inferior. Ya que los círculos primitivos tienen contacto con rodamiento puro, los arcos P1P2P3, Q1P2Q3 son de igual distancia. También por definición, P1P2 es el arco de acceso y P2P3 el arco de receso para el engrane superior, mientras que los arcos Q1P2 y P2Q3 tienen los mismos valores para el engrane inferior. Los ángulos de acceso y receso para ese ultimo se encuentran uniendo P1 y P3 al centro del engrane superior como se ha indicado en la figura; una construcción semejante localiza los ángulos de acceso y receso perteneciente al engrane inferior. El ángulo de presión queda anotado en la figura.

Debe observarse que los puntos F y G, donde empiezan y termina el contacto, se localizan en las intersecciones de los círculos addendum, o círculos e la altura de la cabeza del diente, con las ínea de presión CD. F y G se localizan entre los puntos C y D en esta figura, sin embargo con otras proporciones de los dientes y otro número de dientes en los engranes, puede suceder que cualquiera F o G, o ambas F y G caigan sobre la extensión de CD. Esto tiende a interferir con los dientes.
Propiedades de la evolvente
Las curvas evolventes tienen una ventaja principal sobre las cicloidales y otras curvas que puedan ser empleadas para generar perfiles de engranajes circulares: particularmente, que la distancia de centro a centro puede ser alterada sin destruir la acción conjugada del diente o cambiar la relación de velocidad angular. Es decir, un par de estas curvas cumplirá con la ley fundamental , no importando cual sea la distancia entre centro y centro. La comprobación de lo establecido se puede observar con referencia a la Fig. 9.23. Cuando los centros de los engranes A y B son apartados a una mayor distancia, la tangente común CD a los círculos base se inclinara a un ángulo mayor con EF, por lo tanto se aumentará el ángulo de presión φ. Igual que antes, la tangente común cruzará la línea de centros en un punto fijo, porque todavía estamos tratando con el contacto de las curvas evolventes. Los radios primitivos AP y BP se agrandan, pero el radio de BP a AP permanece sin ningún cambio al igual que los círculos base, que también permanecen sin cambio alguno. No obstante con referencia a la figura,

ahora
Pero BD/AC es independiente de la distancia de cetro a centro. La relación de velocidad, en consecuencia, depende únicamente de los diámetros relativos de los círculos base, y no cambia cuando la distancia de cetro a centro, es alterada.
Una segunda deducción se puede hacer de la Fig. 9.23 y esta es que un perfil evolvente no tienen en si mismo ni círculo primitivo ni algún ángulo de presión en particular, pero tienen ambos a estos en virtud de su localización con referencia a una segunda evolvente. De este modo si un engranaje encaja con otros dos, puede tener dos círculos primitivos de diferentes diámetros, cada uno correspondiente a un contacto. Algunas veces es posible fabricar formas perfeccionadas para el diente haciendo uso de esta propiedad.
Una tercera deducción se puede establecer fácilmente derivando de la geometría de la Fig. 9.23 y esta es que el diámetro del círculo base es igual al diámetro del círculo primitivo multiplicado por el coseno del ángulo de presión.
En vista de que una cremallera puede considerarse como una parte de una rueda dentada con un radio primitivo infinito, el círculo base para la evolvente de la cremallera también tendrá un radio infinito y la evolvente en sí será una línea recta. Los dientes de una cremallera con el sistema evolvente tendrán por esto unas superficies de trabajo rectas. La Fig. 9.24 ilustra un diente para un cremallera de este tipo en el cual el ángulo entre el flanco del diente y la perpendicular a la línea primitiva es igual al ángulo de presión.
Un ángulo de presión de 14.5° fue adoptado primeramente para los dientes de un engrane evolvente. El seno de este ángulo es aproximadamente 0.25, lo cual simplifica el trabajo al trazar los dientes. El mismo ángulo de presión continua empleándose extensivamente, en vista de que comúnmente resultan formas para el diente muy satisfactorias. Ángulos mayores, hasta de 25° son comunes particularmente cuando se requiere un número reducido de dientes.
Las siguientes conclusiones concernientes a la evolvente y su aplicación para los dientes de un engrane se pueden resumir como sigue:
1.- La evolvente o involuta, se determina completamente por el diámetro de su círculo base.
2.-Una evolvente que se mueve alrededor del centro de su círculo base, imparte un movimiento rotativo a una evolvente con la cual hace contacto, con una relación exacta de los diámetros de sus respectivos círculos base.
3.-Una evolvente no tienen ángulo de presión hasta que se efectúe un contacto íntimo con otra evolvente o un cremallera.
4.-El ángulo de presión se determina por la distancia centro y los diámetros del círculo base.
5.- Una vez establecido el ángulo de presión ese es constante para una distancia centro fija.
6.-Una evolvente no tienen diámetro primitivo hasta que se efectúe un contacto íntimo con otra evolvente o una cremallera.
7.- El diámetro primitivo de una evolvente haciendo contacto con otra evolvente, se determina por la distancia centro y la relación.
8.-El ángulo de presión de una evolvente que hace contacto con una cremallera, no cambia cuando el centro del círculo base cambia de posición aproximándose o alejándose de la cremallera.
9.- El diámetro primitivo de una evolvente haciendo contacto con una cremallera, no cambia cuando el centro del círculo base cambia de posición aproximándose o alejándose de la cremallera.
10.- La posición de la línea primitiva del engranaje de una evolvente y una cremallera, se determina por la intersección de la línea de acción y de una línea que pasa a través del centro del círculo base y perpendicular a la dirección de la carrera de la cremallera.
El estudiante debe satisfacerse con referencia a la validez de lo establecido anteriormente y comprenderlo totalmente, ya que forma la base para el diseño de un engranaje evolvente. Ventajas prácticas. Se obtienen con el empleo de la evolvente y se pueden resumir como sigue:
(a) Los engranajes evolventes pueden emplearse con una pequeña falta de precisión inicial en la distancia de centro a centro, o esta distancia puede cambiar como un resultado del desgaste de los cojines, y el contacto de los dientes continúa cumpliendo con la ley fundamental de las ruedas dentadas.
(b) Los engranajes evolventes pueden emplearse para aplicaciones tales como la transmisión de las laminadoras en las fábricas de acero, donde la distancia de centro a centro cambia constantemente.
(c) La superficie de trabajo de la evolvente de una cremallera es de la forma más simple posible: un plano. Esto reduce a una mínimo la dificultad de producir dientes conjugados con exactitud – lo cual es una ventaja de fabricación.
(d) Cuando los dientes son fabricados con el cortador de una fresa, el número necesario de cortadores para cubrir una gama desde el piñón, más pequeño hasta una cremallera, es menor que el necesario para los perfiles cicloidales. Esto se debe al ligero cambio en la curvatura del diente cuando se aumente el número de dientes.
La principal desventaja de los dientes evolventes reside en el hecho que se obtienen interferencia con los piñones que tienen un número reducido de dientes; esto se puede eliminar variando la altura del addendum o altura de la cabeza y del dedendum o altura del pie, de los dientes correspondientes.
Producción de ruedas dentadas
Es importante considerar la manera en que son producidos los dientes. Uno de los primeros procesos fue el de colar en arena la rueda y los dientes. Este método se emplea todavía en los engranajes de bajas velocidades y que quedan expuestos a la intemperie. Es seguro que las superficies del diente se oxiden y se corroan, de tal forma que la falta de precisión inicial tienen muy poco efecto en la acción.
El segundo método para elaborar las superficies es el de la fresadora, que desbasta o corta el espacio entre los dientes. Una fresa que tiene un cortador de la misma forma que el espacio entre los dientes, alimentada con una matriz o forma en blanco, (véase Fig. 9.25) y luego ésta es alineada para el siguiente corte.

Un examen de las figuras de este capítulo que muestran engranajes con un número diferente de dientes engranados, demuestra que la forma de los dientes cambia con el número de dientes del engranaje, no obstante que el paso sea constante. Como un caso extremo, la cremallera evolvente tienen los flancos del diente rectos. Esto es importante, ya que la fuerza del diente está en función de su perfil. Puesto que la forma del diente cambia con el número de dientes en un engrane, un cortador o fresa debe emplearse para cada tamaño de engrane, no obstante que el paso permanezca constante. En la realidad, los cortadores se emplean sobre una gama de números de dientes. Un ejemplo típico de esto se da en la Tabla 9.1 para el sistema de un solo diente. Cada cortador es el correcto para los números mas chicos del grupo y con un poco de error para los números grandes. No obstante, los errores introducidos de esta forma pueden ser parcialmente corregidos variando ligeramente la profundidad del corte sobre la forma en blanco.
Como es difícil obtener altas norma de precisión con los dientes cortados con la fresadora, este tipo se emplea más satisfactoriamente cuando las cargas y las velocidades son moderadas.
Para precisión en engranajes de alta velocidad, el principio generativo es el que ahora se emplea casi por completo. Si una cremallera o un engrane con dientes de un perfil deseado se emplea como cortador, entonces es posible tallar los dientes sobre una matriz con la cual los dientes estarán conjugados. El proceso por el cual los dientes son conformados sobre el segundo engrane puede efectuarse como sigue: Supóngase que la forma en blanco o matriz de la cual se va a cortar está hecho de un material plástico. El engrane y la forma se montan sobre unas flechas y ruedan juntas de tal forma que sus superficies primitivas tengan la
misma velocidad lineal. Entonces los dientes “ se ruedan “ dentro de la superficie blanda de la forma. Estos dientes tendrán el perfil correcto.
El proceso “ generativo “ para cortar dientes de un engrane, comúnmente empleado para producciones comerciales, es llevado a cabo en una forma similar. Por ejemplo, en la matriz “Fellows” para un engrane, la herramienta cortadora toma la forma de un engrane y se pasa a través de la forma en blanco recíprocamente. (Véase la Fig. 9.26).
Entre los recorridos de la máquina herramienta, el cortador y la forma en blanco giran ligeramente, y este movimiento relativo es equivalente al rodamiento de las superficies primitivas.
Los dientes resultantes tendrán la misma forma que los obtenidos por el procedimiento de rodarlos “ hacia adentro” descrito anteriormente, sin el requerimiento de emplear una forma de plástico.
La herramienta cortadora del tipo de cremallera es muy satisfactoria en vista de que sus flancos son rectos, y por lo anterior se puede fabricar fácilmente con exactitud, y también rectificar con facilidad.
La ventaja sobresalientes del método generativo es que el mismo cortador se puede emplear para conformar engranes con cualquier número de dientes, y con mayor precisión que en los método en los cuales el perfil del diente debe de ser rectificados sobre el cortador. Si al cortador se le da un movimiento recíproco a través de la forma en blanco, a cierto ángulo, resultará un engrane helicoidal.
Perfiles de dientes normalizados
En vista de los requerimientos de los perfiles para dientes de engranes, se han hecho patrones o unificado diferentes tipos de dientes. Se tienen normas en sistemas americano y sistema métrico.
Como ejemplo, se presentan cuatro tipos de dientes normados por la Asociación Americana de Normas (FPS) y por la Asociación Americana de Fabricantes de Engranes (AGMA). Estos son conocidos como sigue:
a) Sistemas compuesto de 14 ½°
b) Sistema evolvente de profundidad completa a 14 ½°.
c) Sistema evolvente de profundidad completa a 20°.
d) Sistema de evolvente “despuntada” a 20°.
Las proporciones de los dientes para esos sistemas los muestra la tabla 9.2. Debe notarse que los sistemas compuestos, de profundidad completa a 14 ½° y de profundidad completa a 20° tienen todos los dientes a las mismas proporciones. Estas proporciones son exactamente las mismas que las empleadas anteriormente en el sistema “Brown & Sharpe Standard”.
Cada uno de los cuatro sistema normalizados tienen dientes de engranes, los cuales estas conjugados a una “cremallera básica”. Esta cremallera básica es, por lo anterior, la normalización, patrón o forma de referencia en el desbastado o fresado de dientes sobre engranes de cualquier tamaño.
Sistema compuesto a 14 ½°. Este sistema se desarrolla de los perfiles de dientes cicloidales que hace tiempo se empleaban universalmente. Aproximadamente el tercio central del perfil tiene una forma evolvente, mientras que el resto es de una naturaleza cicloidal. Estos dientes generalmente se producen y se conforman con los cortadores de la fresa, no obstante también se pueden hacer con la fresa matriz. A pesar de que posee algunas ventajas del sistema evolvente, evita la interferencia y el sobrecorte en los engranes chicos los cuales son problemas característicos del aquel sistema cuando se empleaban proporciones de dientes normalizados.
Sistema evolvente de la profundidad completa a 14 ½°. La cremallera básica de este sistema se ilustra en la Fig. 9.27 Este sistema se emplea ampliamente para fabricar dientes de engrane, no obstante la presente tendencia de normalizar sobre el sistema evolvente de profundidad completa a 20°.

Hay interferencia cuando el número de dientes de engranes iguales es menor de 23 o cuando un cremallera engrana con un piñón con menos de 32 dientes. Por lo anterior se hace necesario sobrecortar cuando hay un número reducido de dientes, dando como resultado un arco de acción poco satisfactorio. Por ejemplo con dos engranes de 12 dientes cada uno, el arco de contacto es 0.034 del paso circunferencial, un valor que no se puede emplear. El arco de acción deseado, es decir, 1.4 veces el paso circunferencial, se obtienen con engranes que tienen 20, 21 o 22 dientes, donde el valor exacto depende del número de dientes con el engrane que le hace pareja. Este tipo de dientes es muy satisfactorio, en todo caso, cuando los números de dientes es grande.
Sistema evolvente de profundidad completa a 20°. La cremallera básica (Fig. 9.28) es la misma del sistema de 14 ½°, exceptuando el ángulo de presión. El empleo de un ángulo de presión mayor tiende a mejorar la acción del diente cuando el número de dientes es pequeño. Por ejemplo, se puede obtener un arco de acción igual a 1.4 veces el paso circunferencial con engranes iguales de 14 dientes. A este respecto, el tipo de dientes indicado da los mejores resultados que cualquiera de los cuatro tipos normalizados, cuando se usa un número reducido de dientes. Se emplea para dientes que se tallan con el sistema generativo.

Sistema de evolvente “despuntada” a 20. la cremallera básica tiene un diente alrededor de 18 por ciento más chico que los sistemas de profundidad completa. Las dificultades con la interferencia son mucho más reducidas, comparando con los otros dientes evolventes normalizados. Por esta razón una cremallera con dientes “despuntados” engranará con un piñón de 17 dientes sin ninguna interferencia. Un par de piñones de 12 dientes da un arco de acción igual a 1.19 veces el paso circunferencial. Este es un valor que sí se puede emplear. De cualquier forma, el arco de acción no aumenta rápidamente con el incremento del número de dientes; una combinación 27-30 solamente tienen un valor de 1.35 veces el paso circunferencial.
Por esta razón se hace especialmente importante cortar con precisión si se quiere evitar una acción ruidosa. La Fig. 9.29 muestra una comparación gráfica de un dientes ”despuntado” a 20° con otro a profundidad completa a 14 ½° con el mismo paso para engranes de igual tamaño. El diente más chico con la base más amplia, característica peculiar del anterior, nos da un alta resistencia a través del diente, lo cual explica la conveniencia de emplearlo donde esta sujeto a golpes fuertes.
No obstante que el diente “despuntado” a 20° fue diseñado originalmente para emplearse en las transmisiones de los automóviles ha sido suplantado por el diente de profundidad completa a 20°. Los dientes a profundidad completa son mas largos y es por esto que tienen un arco de acción mayor, y además mucho más número de dientes hacen contacto para soportar la carga. No obstante que la resistencia a través de cada diente es menor, el mayor número de dientes en acción permite sostener cargas mayores.